検定力分析

G*Powerのガイド、 tutrial、 How to Use G*Powerを参考にした。感謝。

概要

  • どの分析をするにせよまず、効果量の算出や変換が必要である。そのため、まず分析の種類ごとに、必要な効果量を特定し、その効果量の算出について記述する。
  • 分析ごとの効果量の指標は以下のとおり
    • t検定: d
    • 分散分析: f
    • 共分散分析: f
    • 相関および重回帰: f
    • 多変量分散分析: f二乗
    • カイ二乗検定: w
  • 効果量には様々なものがあり、t検定ではrとか、分散分析ではイータとかオメガなどがある。しかし、上の効果量を算出もしくは換算しないと検定力分析はできない。
  • 基本的にt分布を用いた検定の検定力には効果量dを、F分布を用いた検定の検定力には効果量fもしくはその二乗をもちいる。デザインごとにdやfの計算方法が異なるが、効果量を算出してしまえば検定力分析の手順は同じ。 (それなのに、なぜイータやオメガを使うのかさっぱりわからん。全部fを使えばいいじゃない)
  • G*Powerでは平均や分散を入力することで上のような効果量を計算してくれる。

検定力分析の種類

  • ある効果量が有意になるサンプルサイズを決めたりする。これを事前 (a priori) の分析ともいう。
    • "平均値差が40msくらいになるらしいけど、これを5%水準で有意にするには参加者を何人集めればいいかな"
  • あるサンプルサイズで有意になる効果量を調べたりする (このサンプルサイズだと、最低このくらいの差が無いと有意にならない、ということを調べる) 。
    • "20人くらいしか参加者集められないけど、平均値差がどのくらいになれば有意になるかしらん"
  • 実験・調査後にその検定力を調べたりする。これを事後 (post hoc) の分析ともいう。

検定力分析分析の4要素

  • 以下の4つのうちいずれか3つがわかれば残りのひとつも得られる。
  • サンプルサイズ (sample size)
  • 効果量 (effect size)
  • 有意水準 = 第1種の過誤の確率 = 有意じゃないのに有意といっちゃう (significance level = P(Type I error) = probability of finding an effect that is not there) 。大体5%未満にされる
  • 検定力 = 1 - 第2種の過誤 = 有意なのを有意という確率 (power = 1 - P(Type II error) = probability of finding an effect that is there. 第2種の過誤自体は有意なのに有意じゃないといっちゃう確率) 。大体80%より上にされる


効果量まとめ

分散分析の効果量

  • f, f2, h2 (イータ二乗) , hp2 (偏イータ二乗) がある。h2, hp2　は標本からの推定値。
  • f2 = f^2 = sigma.effect / sigma.error # 群間分散 / 誤差分散。もしくは群間平方和 / 誤差の平均平方 (mse) * サンプルサイズ。通常の分散分析表で報告される“誤差平方和”はmse*誤差自由度であるが、f2を出すときの分母にこちらを用いる場合もある (非心パラメータを求めるとき)
    • ms.effect / ms.error がいわゆるF値
    • f2 = (ms.effect*df.effect) / (ms.error*df.error) であり、この平方根がfとなる。ただし、分母で誤差自由度をかけるのではなく総サンプルサイズをかける場合もある。
    • f2 = hp2 / (1-hp2) で求めることもある (G*Powerで偏イータ二乗を直接入力してf二乗を求める場合)
  • h2 = ss.effect / ss.total # 群間平方和 / 総平方和
    • # R二乗 (いわゆる決定係数) も同じ式
    • R2 = ss.effect / ss.total
  • hp2 = ss.effect / (ss.effect + ss.error) # 群間平方和 / (群間平方和 + 誤差平方和)
    • # F値と自由度からhp2を求める
    • hp2 = (Fv.effect*df.effect) / (Fv.effect*df.effect+df.error)
    • hp2 = ((Fv*df.effect) / df.error) / (((Fv*df.effect) / df.error) + 1)
  • h2とf2の関係
    • h2 = f2 / (1+f2)
    • f2 = h2 / (1-h2) # R2 = f2 なので、 f2 = R2 / (1-R2) ともできる。
  • w2 (オメガ二乗) 、wp2 (偏オメガ二乗) 。母集団推定値
    • w2 = (ss.effect - df.effect*mse) / (ss.total + mse) # or (ss.effect-ss.error)/ss.effect
    • wp2 = (ss.effect - df.effect*mse) / (ss.effect + (N-df.effect) * mse)

参考
Conventions for Defining Effect Sizes
Effect Size Caluculator

Rで検定力分析

pwr で Cohen (1988)の検定力分析を実行できる。以下関数リスト

関数 計算される検定力
pwr.2p.test 2群の比率差 (各群の人数が等しい)
pwr.2p2n.test 2群の比率差 (各群の人数が異なる)
pwr.anova.test 各群の人数が等しい分散分析 (釣合い型9
pwr.chisq.test カイ二乗検定
pwr.f2.test 一般線形モデル
pwr.p.test 1群の比率 (ある比率が0から有意に離れているか)
pwr.r.test 相関
pwr.t.test t検定 (1群, 2群, 対応のある)
pwr.t2n.test t検定 (2群で各群の人数が異なる)

いずれの関数も効果量、サンプルサイズ、有意水準、検定慮の4つのうち、いずれか3つを指定することで残りの1つを求めることができる。

効果量はきちんと勉強してから計算しましょう。

t検定

t検定用の関数

pwr.t.test(n = , d = , sig.level = , power = , type = c("two.sample", "one.sample", "paired"))

pwr.t2n.test関数は各群のサンプルサイズが異なるとき用の関数。データを収集した後で検定力を調べるのに使う。

t検定の効果量は以下の式で

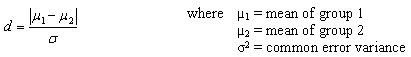
Cohen d

Cohenの効果量dは0.2が小さい、0.5が中程度、0.8が大きい、とされる

"two-sided" (両側検定) がデフォ

使用例

  1. まず2群の平均値差を調べる。先行研究から、平均値差が2.6くらい、各群の (不偏) 分散は11くらいになることがわかっている。先行研究のサンプルサイズは各群20であった。
  2. 平均値差と分散の情報から効果量dを求める。
  3. これで有意水準5%、検定力80%で有意になるにはどのくらいのサンプルサイズかを知りたい。
  4. pwr.t.test関数により効果量、有意水準、検定力からサンプルサイズを求める。

# 心理統計学の基礎 p.163-166の例で
  # 効果量を求めるには事前に平均値差各群のサンプルサイズや分散の情報が必要だが、それは先行研究から調べておく。
  # 先行研究ですでに効果量が報告されていればそのままdvに入力する。

v1 <- 12.576; v2 <- 10.261
n1 <- 20; n2 <- 20
dms <- abs(2.6) # 平均値差
spe <- sqrt(((v1*(n1-1)+v2*(n2-1))/(n1+n2-2))) # プールされた標準偏差
  # プールされた標準偏差を求めるとき、各群のサンプルサイズが等しい場合はサンプルサイズの情報 (n1, n2) を使わず以下でも同じ結果となる
  dms/sqrt((v1+v2)/2)
(dv <- dms/spe) # 効果量

# pwr.t.testを用いてサンプルサイズを求める
library(pwr)
pwr.t.test(d=dv, sig.level=0.05, power=0.80)
# 各群27人以上いればよい


G*Powerの使用例

# ある群の平均値 (15) が特定の値 (10) より離れているとき、有意になるサンプルサイズを調べる。
# Means: Difference from constant (one-sample case)

# 平均値、標準偏差から効果量を求める。
h1 <- 15
sd <- 8
h0 <- 10

# 効果量
(dv <- (h1-h0)/sd)

library(pwr)
pwr.t.test(d=dv, sig.level=0.05, power=0.95, type="one.sample", alternative="greater")
  # 両側検定をするとき   pwr.t.test(d=dv, sig.level=0.05, power=0.95, type="one.sample", alternative="two.sided")


# 独立2群の差でサンプルサイズを求める・検定力を調べる。
# Difference between two independent means (two groups)

# 平均値、標準偏差から効果量を求める。
m1 <- 17
m2 <- 14
sd1 <- 5; v1 <- sd1^2
sd2 <- 4; v2 <- sd2^2
spe <- sqrt(((v1)+(v2))/2) # プールされた標準偏差 参加者数が同じ場合
  # 参加者数が違う場合は以下
  n1 <- 40
  n2 <- 20
  sqrt(((v1*(n1-1)+v2*(n2-1))/(n1+n2-2)))

# 効果量
(dv <- (m1-m2)/spe)

# 効果量、有意水準、検定力を設定し、
# pwr.t.testを用いてサンプルサイズを求める
library(pwr)
pwr.t.test(d=dv, sig.level=0.05, power=0.80)

# 効果量、有意水準、サンプルサイズを設定し、
# pwr.t2.testを用いて検定力を求める
pwr.t2n.test(d=0.8, n1=20, n2=40, sig.level=0.05)
# n1=30, n2=30のとき
pwr.t2n.test(d=0.8, n1=30, n2=30, sig.level=0.05)


# 対応のある群の差の比較で検定力を求める
# Means: Difference between two dependent means (matched pairs)
m1 <- 0
m2 <- 0.4
sd1 <- 1; v1 <- sd1^2
sd2 <- 1; v2 <- sd2^2
ro <- 0.55
spe <- sqrt(v1+v2-(2*ro)*v1*v2) # 対応のあるt検定の場合、本来は差得点の分散を分母に用いる
dv <- abs(m1-m2)/spe
dv # Tutorialではfと表記。

library(pwr)
pwr.t.test(d=dv, sig.level=0.05, n=50, type="paired")



分散分析

G*Powerの例を使う。

pwr.anova.test() でできることははpwr.f2.test() で可能なので気にしない。

1要因参加者間分散分析

１要因参加者間分散分析の検定力分析 (ANOVA: Fixed effects, omnibus, one-way

効果量には f を用いる。

  • f = sqrt(ss.effect / ss.error) = sqrt(f2)
  • 基準としては、0.10=小さい、0.25=中程度、0.40=大きい　とされる。
  • 1要因分散分析の場合、イータ二乗と偏イータ二乗は一致する(総平方和 = 群間平方和 + 誤差平方和) なので。


効果量の算出。G*Powerの例。

# 各群の平均値、サンプルサイズから群間平方和を求める。なんにせよ、郡内分散 (誤差分散) の情報がなければ求めることはできない。
m1 <- 2
m2 <- 3
m3 <- 4
m4 <- 5
ui <- c(m1, m2, m3, m4)
# 各群のサンプルサイズ
n1 <- 2
n2 <- 3
n3 <- 4
n4 <- 4
ni <- c(n1, n2, n3, n4)
wi <- (ni/sum(ni))
mubar <- sum(wi*ui) # 各群のサンプルサイズが等しい場合、mean(ui)
sigma.m <- sqrt(sum(wi*((ui-mubar)^2))) #各群のサンプルサイズが等しい場合、群の平均値の標本標準偏差 sqrt(var(ui)*(3/4)) SD of the group means
sigma <- 6 # 群内標準偏差　SD within each of the k groups

# 効果量f
fv <- sigma.m/sigma
fv # 0.1=小さい、0.25=中程度、0.4=大きい

# イータ二乗
f2 <- fv^2
f2
eta2 <- f2/(1+f2)
eta2


# 郡内分散の情報から偏イータ二乗を求める
# まず群間分散をもとめる
sigma.m^2
# そのうえで群内分散を求める。群内標準偏差の二乗であり、G*Powerの例では36
sigma^2
# 偏イータ二乗
(sigma.m^2) / (sigma.m^2 + sigma^2)
# 以下とは違うので注意
(sigma.m) / (sigma.m + sigma)

G*Powerの例をやってみる。

# pwr.f2.test(u =, v = , f2 = , sig.level = , power =)関数を使う。
# F統計量を出すときのu=分子自由度、v=誤差自由度 (分母自由度) 、sig.level=有意水準、power=検定力。

# 10条件 (10群) でf=.25 (中程度の効果量) が予測できる。有意水準は0.05をクリアし、かつ検定力は0.95としたいとき、各群のサンプルサイズは何人以上か?

library(pwr)
pwr.f2.test(u=9, v=, f2=0.25^2, sig.level=0.05, power=0.95)
# u=分子の自由度、v=分母の自由度 (誤差自由度), f2=効果量。想定したfの値を二乗する
# この関数が出力するのは自由度なので、サンプルサイズとしては条件数で割り切れる380となるだろう。

# pwr.anova.test() 関数でも同じ結果を返す。
# この関数の場合、k,nは自由度ではなくk=条件数、n=各群のサンプルサイズ。またf二乗ではなくfを入力するので注意。
# 各群100人、3群、f=0.20, 有意水準0.05のときの検定力。
pwr.anova.test(k=3, n=10, f=0.20, sig.level=0.05, power=)
pwr.f2.test(u=2, v=27, f2=0.20^2, sig.level=0.05, power=)

# beta/alpha=1 : (1-alpha)=alphaとしたいとき　たとえば有意確率0.05であればpower=0.95だと1になる
pwr.f2.test(u=9, v=190, f2=0.25^2, sig.level=0.159194)

1要因参加者内分散分析

効果量には f を用いる。f = ss.effect / ss.error である。参加者内デザインであってもF分布を用いて検定しているので、F値を算出した平方和、自由度の情報を使えばよい。

# 吉田・森 (1990) p92の例
# 分散から効果量fを求める　From variances
ss.effect <- 217.5 # Variance explained by effect
ss.error <- 71 # Error variance
fv <- sqrt(ss.effect/ss.error) # Calculate
fv
  # 偏イータ二乗からfを求める。 Direct (おそらくspssでは偏イータ二乗が出力されるためだろう)
    h2 <- 0.7538995
    fv <- sqrt(h2/(1-h2))
    fv

library(pwr)
pwr.f2.test2(u=3, v=21, f2=fv^2, samplesize=8, sig.level=0.05)


多変量分散分析の場合



2要因参加者間分散分析

2要因参加者間分散分析の検定力分析。主効果と交互作用。 (ANOVA: Fixed effects, special, main effects and interactions)

# このサイトのspssの例をもとに、Rで検定力分析を行う。

dat <- read.csv("dat.csv")
mod <- lm(score~drive*reward, contrasts=list(reward=contr.sum, drive=contr.sum), data=dat)
library(car)
fit <- Anova(mod, type=3)
Ares <- Astat(fit)
Ares

# オブジェクトAresからf2を取り出し、pwr.f2.testを用いて検定力を求める
f2s <- Ares$efs[2:4,2]
numdf <- Ares$unv[2:4,2]
dendf <- Ares$unv[5,2]
library(pwr)
# drive要因の検定力
pwr.f2.test(u=numdf[1], v=dendf, f2=f2s[1], power=)
# reward要因の検定力
pwr.f2.test(u=numdf[2], v=dendf, f2=f2s[2], power=)
# 交互作用の検定力
pwr.f2.test(u=numdf[3], v=dendf, f2=f2s[3], power=)

# この結果は参考ページのものと一致しない。また、2元配置参加者間デザインの場合、pwr.f2.testの結果はspssともG*Powerとも一致しない。
# この原因は2点あり、spssの検定力分析はf二乗と非心パラメータがサンプルサイズに基づいているからである。Astat関数やpwr.f2.test関数はf二乗や非心パラメータがサンプルサイズではなく自由度を用いて計算している。
  # pwr.f2.testの非心パラメータlambdaは　lambda <- f2 * (u + v + 1)　で計算されている。uは要因の自由度、vは誤差自由度だが、u+v+1がサンプルサイズに一致するのは1元配置の分散分析だけだろう。修正してpwr.f2.test2という関数にした。サンプルサイズの入力が必要。

# したがって、spssおよびG*Powerにあうように計算するにはまずf二乗を計算しなおす。
numss <- Ares$unv[2:4, 1] # 分子の平方和はそのまま
denss <- (Ares$unv[5, 1]/Ares$unv[5, 2])*sum(Ares$unv[,2]) # 分子は平方和ではなく標本分散*サンプルサイズとする。そのため、いったん平均平方和をだしてそこにサンプルサイズ (自由度の総計) をかける
f2s.2 <- numss/denss
f2s.2
sqrt(f2s.2) # このfの値および自由度を用いればG*Powerの出力とも一致する。
  # Input
    # Effect size f: 0.2335497
    # α err prob: 0.05
    # Total sample size: 24
    # Numerator df: 1
    # Number of groups: 6
# 非心パラメータを計算しなおす。f二乗*N (全体のサンプルサイズ) となる
lambdas <- f2s.2*sum(Ares$unv[,2])
# 検定力を計算しなおす
  pf(qf(0.05, numdf[1], dendf, lower = FALSE), numdf[1], dendf, lambdas[1], lower = FALSE)
  pf(qf(0.05, numdf[2], dendf, lower = FALSE), numdf[2], dendf, lambdas[2], lower = FALSE)
  pf(qf(0.05, numdf[3], dendf, lower = FALSE), numdf[3], dendf, lambdas[3], lower = FALSE)

# pwr.f2.test2関数を使う
N <- sum(Ares$unv[,2])
# drive要因の検定力
  pwr.f2.test2(u=numdf[1], v=dendf, samplesize=N, f2=f2s.2[1], power=)
# reward要因の検定力
  pwr.f2.test2(u=numdf[2], v=dendf, samplesize=N, f2=f2s.2[2], power=)
# 交互作用の検定力
  pwr.f2.test2(u=numdf[3], v=dendf, samplesize=N, f2=f2s.2[3], power=)

# G*Powerの例もやってみる。
fv <- 0.7066856
f2 <- fv^2
pwr.f2.test(u=2, v=72, f2=f2, sig.level=0.05, power=)
# lambdaを計算しなおしてやりなおす。
lmda <- f2*108
pf(qf(0.05, 2, 72, lower = FALSE), 2, 72, lmda, lower = FALSE) # こっちが一致する。
N <- 108
pwr.f2.test2(u=2, v=72, samplesize=N, f2=f2, sig.level=0.05)



Correlations

For correlation coefficients use

pwr.r.test(n = , r = , sig.level = , power = )

where n is the sample size and r is the correlation. We use the population correlation coefficient as the effect size measure. Cohen suggests that r values of 0.1, 0.3, and 0.5 represent small, medium, and large effect sizes respectively.

Linear Models

For linear models (e.g., multiple regression) use

pwr.f2.test(u =, v = , f2 = , sig.level = , power = )

where u and v are the numerator and denominator degrees of freedom. We use f2 as the effect size measure.

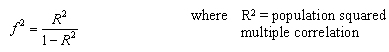
cohen f2

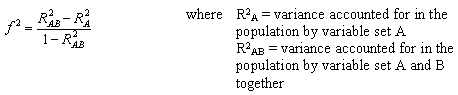
Cohen f2 alternate

The first formula is appropriate when we are evaluating the impact of a set of predictors on an outcome. The second formula is appropriate when we are evaluating the impact of one set of predictors above and beyond a second set of predictors (or covariates). Cohen suggests f2 values of 0.02, 0.15, and 0.35 represent small, medium, and large effect sizes.

Tests of Proportions

When comparing two proportions use

pwr.2p.test(h = , n = , sig.level =, power = )

where h is the effect size and n is the common sample size in each group.

Cohen h

Cohen suggests that h values of 0.2, 0.5, and 0.8 represent small, medium, and large effect sizes respectively.

For unequal n's use

pwr.2p2n.test(h = , n1 = , n2 = , sig.level = , power = )

To test a single proportion use

pwr.p.test(h = , n = , sig.level = power = )

For both two sample and one sample proportion tests, you can specify alternative="two.sided", "less", or "greater" to indicate a two-tailed, or one-tailed test. A two tailed test is the default.

Chi-square Tests

For chi-square tests use

pwr.chisq.test(w =, N = , df = , sig.level =, power = )

where w is the effect size, N is the total sample size, and df is the degrees of freedom. The effect size w is defined as

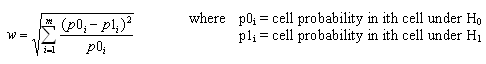
Cohen w

Cohen suggests that w values of 0.1, 0.1, and 0.5 represent small, medium, and large effect sizes respectively.

some Examples

library(pwr)

# For a one-way ANOVA comparing 5 groups, calculate the
# sample size needed in each group to obtain a power of
# 0.80, when the effect size is moderate (0.25) and a
# significance level of 0.05 is employed.

pwr.anova.test(k=5,f=.25,sig.level=.05,power=.8)

# What is the power of a one-tailed t-test, with a
# significance level of 0.01, 25 people in each group,
# and an effect size equal to 0.75?

pwr.t.test(n=25,d=0.75,sig.level=.01,alternative="greater")

# Using a two-tailed test proportions, and assuming a
# significance level of 0.01 and a common sample size of
# 30 for each proportion, what effect size can be detected
# with a power of .75?

pwr.2p.test(n=30,sig.level=0.01,power=0.75)

Creating Power or Sample Size Plots

The functions in the pwr package can be used to generate power and sample size graphs.

# Plot sample size curves for detecting correlations of
# various sizes.

library(pwr)

# range of correlations
r <- seq(.1,.5,.01)
nr <- length(r)

# power values
p <- seq(.4,.9,.1)
np <- length(p)

# obtain sample sizes
samsize <- array(numeric(nr*np), dim=c(nr,np))
for (i in 1:np){
  for (j in 1:nr){
    result <- pwr.r.test(n = NULL, r = r[j],
    sig.level = .05, power = p[i],
    alternative = "two.sided")
    samsize[j,i] <- ceiling(result$n)
  }
}

# set up graph
xrange <- range(r)
yrange <- round(range(samsize))
colors <- rainbow(length(p))
plot(xrange, yrange, type="n",
  xlab="Correlation Coefficient (r)",
  ylab="Sample Size (n)" )

# add power curves
for (i in 1:np){
  lines(r, samsize[,i], type="l", lwd=2, col=colors[i])
}

# add annotation (grid lines, title, legend)
abline(v=0, h=seq(0,yrange[2],50), lty=2, col="grey89")
abline(h=0, v=seq(xrange[1],xrange[2],.02), lty=2,
   col="grey89")
title("Sample Size Estimation for Correlation Studies\n
  Sig=0.05 (Two-tailed)")
legend("topright", title="Power", as.character(p),
   fill=colors)

sample size curves click to view

 

リンク