仮定の査定
回帰モデルの仮定
- zero-mean: 誤差はランダムな変数で平均ゼロ
- constant variance: 誤差項の分散は定数、独立変数とは無関連
- independent: 誤差項はほかの誤差とは独立
- normality: 誤差は正規分布
分散分析における仮定の検証法を紹介する。回帰診断については重回帰分析 を参照。
外れ値
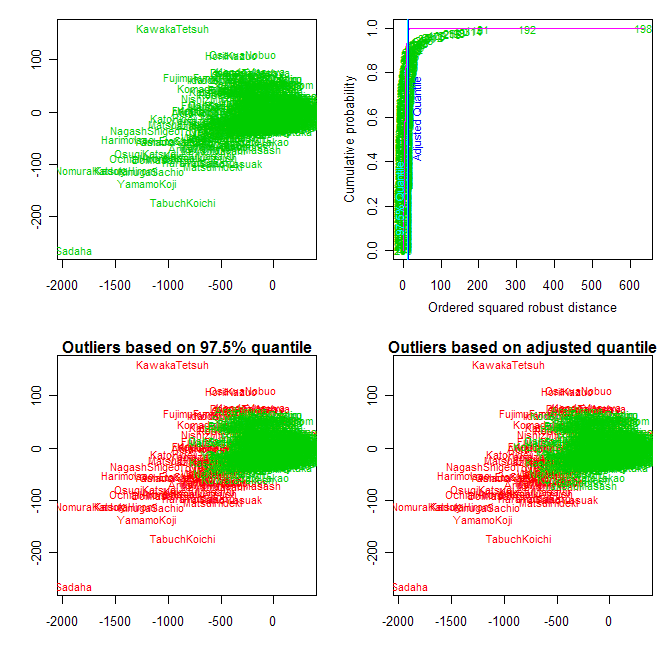
外れ値は正規性と分散の等質性に影響する。 mvoutlier パッケージのaq.plot() 関数はマハラノビス距離をプロットして多変量データの外れ値データを検出できる。入力は行列またはデータフレームをあたえ、4つのグラフとそれぞれのケース (行) が外れ値か否かのTRUE/FALSEがかえされる。
# 打撃成績データ (打率、打点、ホームラン、出塁率、長打率) の外れ値を調べる
dat <- read.delim("http://eau.uijin.com/about/datasets/batting.dat")
rownames(dat) <- dat[,1]
x <- subset(dat, G>1000)[c("AVG", "RBI", "HR","OBP", "SLG")] # 1,000試合超出場選手の打率・打点・本塁打・出塁率・長打率
library(mvoutlier)
outliers <- aq.plot(x)
outliers
# 赤字が外れ値と判定されたデータ。王貞治はすごい。
click to view
単変量データの正規性
Q-Q plotを描いてみよう。
# 上の打撃データから打率と本塁打のQ-Qプロットを描いてみる。
avg <- x$AVG
hr <- x$HR
par(mfrow=c(1,2))
qqnorm(avg)
qqline(avg)
qqnorm(hr)
qqline(hr)
# 打率は正規分布だが、本塁打はゆがんでいる。
click to view
ラインから際立って離れていれば正規性仮定が崩れていることを示す。 shapiro.test() 関数でも正規性を検定できる。p < .05 であれば正規分布から有意に乖離していることを示す。 そのほか、nortest パッケージにもいろいろな関数がある。
多変量正規性
多変量分散分析 (MANOVA) は多変量正規性を仮定している。mvnormtest パッケージの mshapiro.test( ) 関数は多変量正規性のShapiro-Wilk検定を実行できる。数値のみの行列を入力として与える。
library(mvnormtest)
mshapiro.test(t(x)) # t()関数で転置し、行に変数、列にケースがくるようにする。
p x 1 の多変量正規データ 
があるとき、x and μ のマハラノビス距離の二乗は自由度pのカイ二乗分布に従う。これをもとにQ-Qプロットで多変量正規性の査定を行える。
x <- as.matrix(x) # n x p 数値行列
center <- colMeans(x) # 中心化
n <- nrow(x); p <- ncol(x); cov <- cov(x);
d <- mahalanobis(x,center,cov) # distances
qqplot(qchisq(ppoints(n),df=p),d,
main="QQ Plot Assessing Multivariate Normality",
ylab="Mahalanobis D2")
abline(a=0,b=1)
click to view
分散の等質性
bartlett.test( ) : K標本法による等分散性の検定。
fligner.test( ) : 上のノンパラ版。
以下の例はyが数値、gが群変数。
y <- iris[,1]
g <- iris[,5]
# Bartlett 検定
bartlett.test(y~g)
# Figner-Killeen 検定
fligner.test(y~g)
HH パッケージのplot.hov( ) 関数は等分散性のBrown-Forsyth検定にもとづいたプロットが行える。
以下の例はyが数値、gが群変数。gは因子変数でなくてはならない。
y <- iris[,1]
g <- iris[,5]
library(HH)
hov(y~g)
plot.hov(y~g)
click to view
共分散行列の等質性
多変量分散分析や判別分析は分散-共分散行列の等質性を仮定している。これには Box's M 検定を使う。ただしこの検定は敏感すぎてたいていの場合等質性が崩れているとされてしまう (だからこの検定はしなくていいという意見もある) 。RでBoxのM検定を行うにはRhelpの投稿か、青木先生の関数を感謝しながら利用する。